Discontinuous Limits and Continuous Limits Worksheet

Error : Please Click on "Not a robot", then try downloading again.
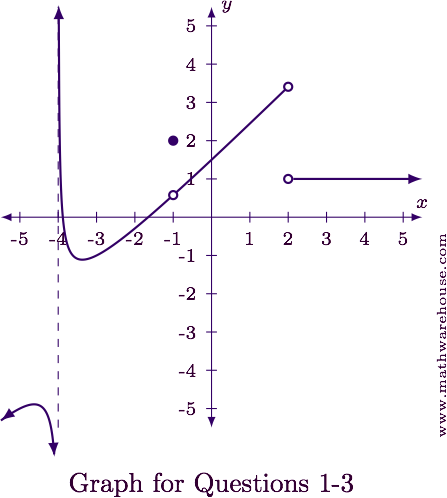
Step 1
Examine the one-sided limits.
- As $$x \to -4$$ from the left, we can see the function is heading downward. The arrow tells us the function is going to continue going downward infinitely.
- As $$x \to -4$$ from the right, the same thing is happening, but in the positive direction.
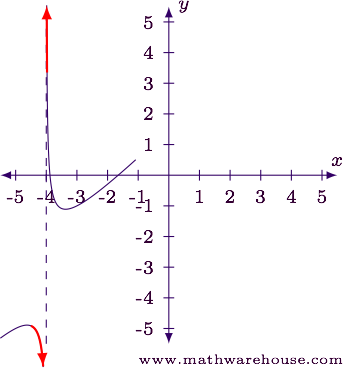
Answer
The function appears to have an infinite discontinuity at x = -4.
Step 1
- As $$x \to -1$$ from the left, we can see the function is heading to roughly $$y = \frac 1 2$$.
- As $$x \to -1$$ from the right, the same thing is happening. The function appears to be headed towards $$y = \frac 1 2$$.
- At $$x = -1$$ the function is defined and has a value of $$f(-1) = 2$$.
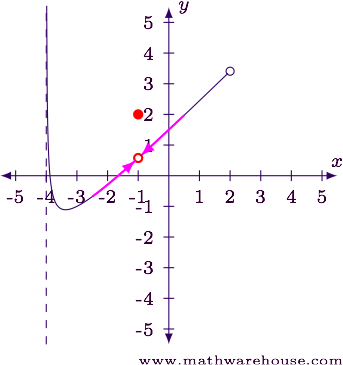
Answer
The function has a removable discontinuity at $$x = -1$$.
Step 1
- As $$x\to 2$$ from the left, we can see the function is heading to roughly $$y = 3.5$$.
- As $$x \to 2$$ from the right, the function appears to be headed towards $$y = 1$$.
- At $$x = 2$$ the function is undefined.
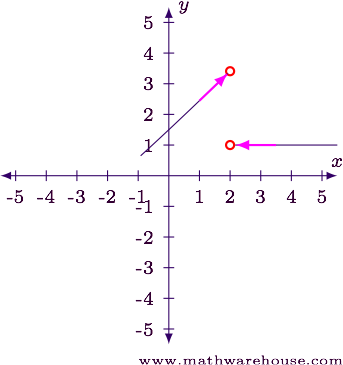
Answer
The function appears to have a jump discontinuity at $$x = 2$$.
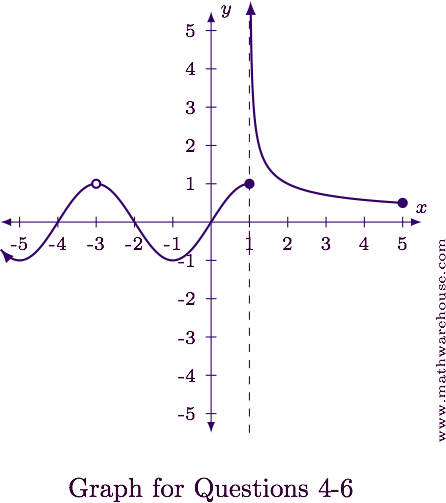
Step 1
- As $$x\to -3$$ from the left, we can see the function seems to be heading to $$y = 1$$.
- As $$x \to -3$$ from the right, the same thing is happening. The function appears to be headed towards $$y = 1$$.
- At $$x = -3$$ the function is undefined.
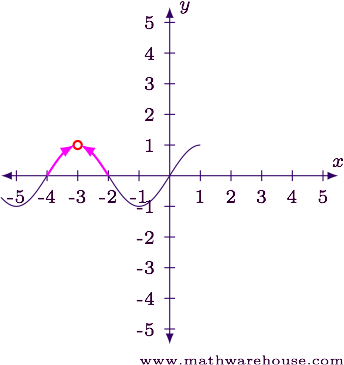
Answer
The function appears to have a removable discontinuity at $$x = -3$$.
Step 1
- As $$x \to 1$$ from the left, we can see the function seems to be heading to $$y = 1$$.
- As $$x \to 1$$ from the right, the function grows infinitely large.
- At $$x = 1$$ the function has a value of $$f(1) = 1$$.
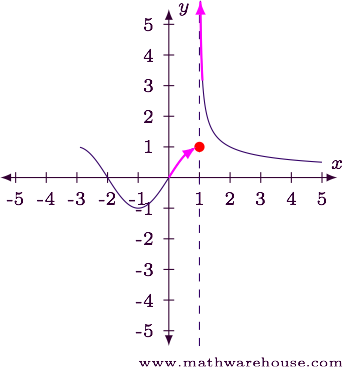
Answer
The function appears to have a mixed discontinuity at $$x = 1$$.
Step 1
- As $$x\to 5$$ from the left, we can see the function seems to be heading to about $$y = \frac 1 2$$ .
- According to the graph, the function is not defined to the right of $$x = 5$$ .
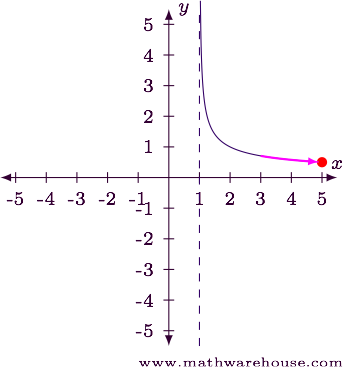
Answer
The function appears to have an endpoint discontinuity at $$x=5$$.
Step 1
From the left: As $$x\to 8^-$$, the left-hand table implies the function is approaching 1.3.
From the right: As $$x\to 8^+$$, the right-hand table implies the function is approaching 5.
Answer
Since the two one-sided limits appear to be different, we conclude the function likely has a jump discontinuity at $$x=8$$.
$$ \begin{array}{c|lcc|l} {x} & {f(x)} \\ \hline 7.9 & 1.36\\ 7.99 & 1.306\\ 7.999 & 1.3006\\ 7.9999 & 1.30006\\ 7.99999 & 1.300006 \end{array} $$
$$ \begin{array}{c|lcc|l} {x} & {f(x)}\\ \hline 8.1 & 4\\ 8.01 & 4.9\\ 8.001 & 4.95\\ 8.0001& 4.995\\ 8.00001 & 4.9995 \end{array} $$
Step 1
From the left: As $$x \to -6^-$$, the table on the left implies $$f(x)$$ is approaching 5.9.
From the right: As $$x\to -6^+$$, the table on the right implies $$f(x)$$ is approaching -2.
Answer
The tables imply the one-sided limits have different values. So we conclude there is likely a jump discontinuity at $$x = -6$$.
$$ \begin{array}{c|lcc|l} {x} & {f(x)} \\ \hline -6.5 & 5.8\\ -6.05 & 5.89\\ -6.005 & 5.899\\ -6.0005 & 5.8999\\ -6.00005 & 5.89999 \end{array} $$
$$ \begin{array}{c|lcc|l} {x} &{f(x)}\\ \hline -5.9 & -2.1\\ -5.99 & -2.01\\ -5.999 & -2.001\\ -5.9999& -2.0001\\ -5.99999 & -2.00001 \end{array} $$
Step 1
Left-hand limit: As $$x$$ approaches 9 from the left, the tables imply $$f(x)$$ is approaching 24.
Right-hand limit: As $$x$$ approaches 9 from the right, the tables imply $$f(x)$$ approaches 24
Answer
The tables imply the limit exists as $$x$$ approaches 9, however the function is undefined there. We conclude the function likely has a removable discontinuity at $$x = 9$$.
$$ \begin{array}{c|lcc|l} {x} & {f(x)} \\ \hline 8.9 & 24.3\\ 8.99 & 24.03\\ 8.999 & 24.003\\ 8.9999 & 24.0003\\ 8.99999 & 24.00003 \end{array} $$
$$ \begin{array}{c|lcc|l} {x} & {f(x)}\\ \hline 9.1 & 24.6\\ 9.01 & 24.06\\ 9.001 & 24.006\\ 9.0001 & 24.0006\\ 9.00001 & 24.00006 \end{array} $$
Step 1
Left-hand limit: As $$x$$ approaches $$\frac 1 2$$ from the left, the tables imply $$f(x)$$ approaches 7.
Right-hand limit: As $$x$$ approaches $$\frac 1 2$$ from the right, the tables imply $$f(x)$$ approaches 7.
Answer
The tables imply the limit exists and is equal to 7, but we know the function value is $$f(1/2) = 4$$. Since the limit and the function have different values, we conclude the function has a removable discontinuity at $$x = \frac 1 2$$.
$$ \begin{array}{c|lcc|l} {x} & {f(x)} \\ \hline 0.40 & 6.9\\ 0.49 & 6.99\\ 0.499 & 6.999\\ 0.4999 & 6.9999\\ 0.49999 & 6.99999 \end{array} $$
$$ \begin{array}{c|lcc|l} {x} & {f(x)}\\ \hline 0.6 & 7.25\\ 0.55 & 7.025\\ 0.505 & 7.0025\\ 0.5005 & 7.00025\\ 0.50005 & 7.000025 \end{array} $$
Step 1
Examine the limit from the left.
$$ \displaystyle\lim_{x\to 11^-} f(x) = \displaystyle\lim_{x\to 11^-} (3x + 1) = 3(11) + 1 = 34 $$
Step 2
Examine the limit from the right.
$$ \displaystyle\lim_{x\to 11^+} f(x) = \displaystyle\lim_{x\to 11^+} (4x-2) = 4(11) -2 = 44 - 2 = 42 $$
Answer
The function has a jump discontinuity at $$x = 11$$.
Step 1
Examine the left-hand limit.
$$ \displaystyle\lim_{x\to-2^-} f(x) = \displaystyle\lim_{x\to-2^-} \sqrt{x+6} = \sqrt{-2 + 6} = \sqrt 4 = 2 $$
Step 2
Examine the right-hand limit.
$$ \displaystyle\lim_{x\to-2^+} f(x) = \displaystyle\lim_{x\to-2^+} -x^2 = -(-2)^2 = -4 $$
Answer
The one-sided limits are different, so the function has a jump discontinuity at $$x = -2$$.
Step 1
Examine the limit from the left.
$$ \displaystyle\lim_{x\to 3^-} f(x) = \displaystyle\lim_{x\to 3^-} |x| = |3| = 3 $$
Step 2
Examine the limit from the right.
$$ \displaystyle\lim_{x\to 3^-} f(x) = \displaystyle\lim_{x\to 3^-} (4x+2) = 4(3)+2 = 12 +2 = 14 $$
Answer
Since the one-sided limits are different, the function has a jump discontinuity at $$x = 3$$.
Step 1
$$ \begin{align*} \lim_{x\to 0^-} f(x) = \lim_{x\to 0^-} x^{1/3} = 0^{1/3} = 0\\[6pt] \lim_{x\to 0^+} f(x) = \lim_{x\to 0^+} x^{1/2} = 0^{1/2} = 0 \end{align*} $$
Step 2
Examine the function value at $$x = 0$$.
$$ f(0)\mbox{ is undefined.} $$
Answer
The one-sided limits are the same, so the limit exists. But since the function is undefined, it has a removable discontinuity at $$x = 0$$.
Step 1
$$ \begin{align*} \lim_{x\to 4^-} f(x) & = \lim_{x\to 4^-} \sin\left(\frac \pi 8 x\right) = \sin\frac \pi 2 = 1\\[6pt] \lim_{x\to 4^+} f(x) & = \lim_{x\to 4^+} \cos(x-4) =\cos(4-4) = \cos 0 = 1 \end{align*} $$
Answer
The limit value is 1, but the function value is 2. Since the limit and the function have different values, the function has a removable discontinuity at $$x = 4$$.
Step 1
$$ \begin{align*} \lim_{x\to 1^-} f(x) & = \lim_{x\to 1^-} e^{x-1} = e^{1-1} = e^0 = 1\\[6pt] \lim_{x\to 1^-} f(x) & = \lim_{x\to 1^-} -\cos(\pi x) = -\cos \pi = -(-1) = 1 \end{align*} $$
Answer
The limit value is 1, but the function value is $$f(1) = 0$$. Since the limit and function values are different, there is a removable discontinuity at $$x = 1$$.
Step 1
Examine the limit from the left.
- The limit has the form of $$\lim\limits_{x\to 1^-} f(x) = \frac 1 0$$.
The limit from the left is infinite.
Step 2
Examine the limit from the right.
- The limit has the form of $$\lim\limits_{x\to 1^+} f(x) = \frac 1 0$$.
The limit from the right is infinite.
Answer
Since both one-sided limits are infinite, the function has an infinite discontinuity at $$x = 1$$.
Step 1
Examine the limit from the left.
$$ \begin{align*} \lim_{x\to0^-} f(x) & = \lim_{x\to0^-} \cot x\\[6pt] & = \lim_{x\to0^-} \frac{\cos x}{\sin x}\\[6pt] & = \frac{\cos 0}{\sin 0}\\[6pt] & = \frac 1 0 \end{align*} $$
This tells us $$\lim\limits_{x\to0^-} f(x)$$ is infinite.
Step 2
Examine the limit from the right.
$$ \displaystyle\lim_{x\to0^+} f(x) = \displaystyle\lim_{x\to0^+} \ln x = -\infty $$
Answer
Since both one-sided limits are infinite, the function has an infinite discontinuity at $$x = 0$$.
Step 1
$$ \begin{align*} \lim_{x\to 4^-} f(x) & \lim_{x\to4^-} (x+3) = 4 + 3 = 7\\[6pt] \lim_{x\to 4^+} f(x) & \lim_{x\to4^+} (x^2-9) = (4)^2 - 9 = 7\ \end{align*} $$
Answer
Since the limit value and function value are the same, the function is continuous at $$x = 4$$.
Step 1
$$ \begin{align*} \lim_{x\to-1^-} f(x) & = \lim_{x\to-1^-} (2x+5) = 2(-1) + 5 = 3\\[6pt] \lim_{x\to-1^+} f(x) & = \lim_{x\to-1^+} (2 - x) = 2 - (-1) = 3 \end{align*} $$
Step 2
Examine the function value at $$x = -1$$.
$$ f(-1) = 2 - (-1) = 3 $$
Answer
Since the limit values and function value are the same, the function is continuous at $$x = -1$$.
Step 1
Examine the function for places where it will be undefined. This is similar to finding the domain of the function.
Since the function is rational, it will be undefined where the denominator is zero. In this case, at $$x = -6$$.
Step 2
Determine the form of the limit as $$x$$ approaches -6.
$$ \lim_{x\to-6} f(x) = \frac{(-6)^2 + 5(-6) - 6}{(-6) + 6} = \frac{36 -30 - 6}{-6 + 6} = \frac{0}{0} $$
With the $$\frac 0 0$$ form this function either has a removable discontinuity (if the limit exists) or an infinite discontinuity (if the one-sided limits are infinite) at -6.
Step 3
Find and divide out any common factors.
$$ \frac{x^2 + 5x - 6}{x + 6} = \frac{\blue{(x+6)}(x-1)}{\blue{x + 6}} = x-1 $$
Step 4
Evaluate the limit of this simpler function.
$$ \displaystyle\lim_{x\to-6} (x-1) = -6-1 = -7 $$
Answer
Since the limit at $$x = -6$$ exists, but the function does not, the function has a removable discontinuity there.
Step 1
Determine $$f(0)$$
$$ f(0) = \frac{\sin 0}{2(0)^2 + 5(0)} = \frac 0 0 $$
This tells us the function is undefined at $$x = 0$$.
Step 2
Determine whether or not the limit exists at $$x = 0$$.
Examine the limit as $$x$$ approaches 0.
$$ \lim_{x\to 0} f(x) = \frac{\sin 0}{2(0)^2 + 5(0)} = \frac 0 0 $$
With this form, we know the limit might exist. Using the techniques from earlier lessons (see Indeterminate Limits---Sine Forms), we evaluate the limit as follows:
$$ \begin{align*} \lim_{x\to 0} f(x) & = \lim_{x\to0} \frac{\sin 4x}{2x^2 + 5x}\\[6pt] & = \lim_{x\to0} \frac{\sin 4x}{x(2x + 5)}\\[6pt] & = \lim_{x\to0} \frac{\sin 4x} x \cdot \frac 1 {2x + 5}\\[6pt] & = \lim_{x\to0} \frac{\blue 4}{\blue 4}\cdot\frac{\sin 4x} x \cdot \frac 1 {2x + 5}\\[6pt] & = \lim_{x\to0} \frac{\blue 4} 1\cdot \frac{\sin 4x}{\blue 4 x} \cdot \frac 1 {2x + 5}\\[6pt] & = \blue 4 \cdot\red{\lim_{x\to0} \frac{\sin 4x}{4x}} \cdot \frac 1 {2x + 5}\\[6pt] & = \blue 4 \cdot \red{1} \cdot \frac 1 {2(0) + 5}\\[6pt] & = \frac 4 5 \end{align*} $$
Answer
At $$x = 0$$, the limit exists, but the function does not. This means the function has a removable discontinuity at $$x = 0$$.
Step 1
Identify the points where the function is undefined.
This function is undefined at $$x = -7$$.
Step 2
Examine the form of the limit at $$x = -7$$.
$$ \displaystyle\lim_{x\to-7} f(x) = \frac{2(-7) -3}{0} = \frac{-17} 0 $$
Answer
The $$\frac n 0$$ form indicates the function has an infinite discontinuity at $$x = -7$$.
Step 1
Determine where the function is undefined.
Since we are restricted to $$0\leq x \leq \frac \pi 2$$, we can determine that the denominator is equal to 0 only when
$$ \begin{align*} 1 - \cos 3x & = 0\\ \cos 3x & = 1\\ 3x & = 0\\ x & = 0\\ \end{align*} $$
(The denominator is also equal to zero when $$x = \frac{2n\pi} 3$$ for integer values of $$n$$, but these are outside the bounds set for $$x$$.)
Step 2
Determine the form of the limit from the right at $$x=0$$ (note that the limit from the left doesn't exist since that is outside the bounds allowed for $$x$$).
$$ \lim_{x\to0^+} f(x) = \frac{(0)^2 + 9(0)}{1 - \cos 0} = \frac 0 0 $$
Step 3
$$ \begin{align*} \lim_{x\to0^+} \frac{x^2 + 9x}{1-\cos 3x} & = \lim_{x\to0^+} \frac{x(x + 9)}{1-\cos x3x}\\[6pt] & = \lim_{x\to0^+} \frac x {1-\cos 3x}\cdot \frac{x + 9} 1\\[6pt] & = \lim_{x\to0^+} \frac{\blue 3}{\blue 3}\cdot \frac x {1-\cos 3x}\cdot \frac{x + 9} 1\\[6pt] & = \lim_{x\to0^+} \frac 1 {\blue 3}\cdot \frac{\blue 3 x} {1-\cos 3x}\cdot \frac{x + 9} 1\\[6pt] & = \lim_{x\to0^+} \frac{\blue 3 x} {1-\cos 3x}\cdot \frac{x + 9} {\blue 3}\\[6pt] & = \lim_{x\to0^+} \red{\frac{3x} {1-\cos 3x}}\cdot \frac{x + 9} 3\\[6pt] & = \red{\frac 1 0}\cdot \frac{0 + 9} 3\\[6pt] & = \frac 9 0 \end{align*} $$
(Since $$\lim_{\theta\to 0} \frac{1 - \cos \theta}{\theta} = 0 = \frac 0 1$$, we know $$\lim_{\theta\to 0} \red{\frac{\theta}{1 - \cos \theta}} = \red{\frac 1 0}$$)
Answer
The limit has an infinite discontinuity at $$x = 0$$.
Step 1
What is the domain of the function?
The function is defined at all $$x\geq 0$$.
Step 2
Determine the limit as $$x$$ approaches 0 from the right.
$$ \displaystyle\lim_{x\to 0^+}\frac{\sqrt x}{x^2+1} = \frac{ \sqrt 0} 1 = 0 $$
Step 3
Determine the value of $$f(0)$$.
$$ f(0) = \frac{\sqrt 0}{0+1} = 0 $$
Answer
At $$x=0$$, the limit from the right exists and is equal to the function value. Consequently, the function has an endpoint discontinuity at $$x=0$$. We could also say the function is continuous from the right.
Step 1
At $$x = 0$$
- $$f(0) = |0 + 2| = 2$$
- $$\lim\limits_{x\to0^+} f(x) = |0+2| = 2$$
Since the function and the limit value are the same, the function has an end-point discontinuity at $$x = 0$$.
Step 2
At $$x = 8$$
- $$\lim\limits_{x\to8^-} f(x) = 6 - (8 - 4)^2 = 6 - 16 = -10$$
Since the limit exists at $$x = 8$$ we could call this a removable discontinuity which, if fixed, would still be an endpoint discontinuity.
Step 3
At $$x = 4$$
- $$\displaystyle\lim_{x\to4^-} f(x) = |4+2| = 6$$
- $$\displaystyle\lim_{x\to 4^+} f(x) = 6 - (4-4)^2 = 6$$
- $$f(4) = 6 - (4-4)^2 = 6$$
Since $$f(4) = \lim\limits_{x\to4} f(x)$$, we know the function is continuous at $$x = 4$$.
Answer
The function has endpoint discontinuities at $$x = 0$$ and $$x = 8$$.
Return to lesson

Error : Please Click on "Not a robot", then try downloading again.
Source: https://www.mathwarehouse.com/calculus/continuity/how-to-classify-discontinuities-practice-problems.php
Enregistrer un commentaire for "Discontinuous Limits and Continuous Limits Worksheet"